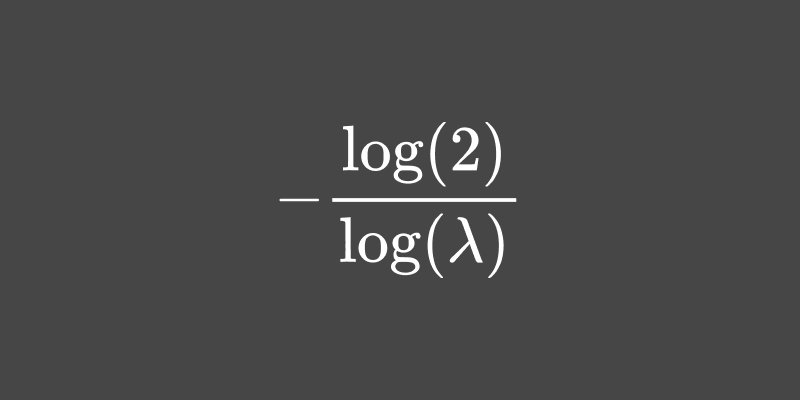I am frequently calculating the half-life of a series to use in mean reversion models. I came across this Stack Exchange answer which showed the derivation of a series half-life based on a regressible model. This is such a common calculation for me that I’ve written out the derivation here so that I never forget.
Model
Define the weakly stationary process \(X\) as: $$ \begin{align} X_t = c + \lambda X_{t-1} + \epsilon_t, \quad 0 < \lambda < 1 \label{1} \end{align} $$
Estimate \(c\) and \(\lambda\) with linear regression.
Distance to the mean
Weak stationarity means that the process \(X\) has a fixed mean: $$ E[X] = \mu $$ Taking the expected value of \(X_t\) we get: $$ \begin{aligned} E[X_t] &= E[c + \lambda X_{t-1} + \epsilon_t] \\ \mu &= c + \lambda E[X_{t-1}] \\ \mu &= c + \lambda\mu \\ \mu &= \frac{c}{1 - \lambda} \\ \end{aligned} $$ Rearranging for \(c\) gives: $$ c = \mu(1 - \lambda) $$
Putting this into \((\ref{1})\) gives: $$ \begin{aligned} X_t &= \mu(1 - \lambda) + \lambda X_{t-1} + \epsilon_t \\ &= \mu + \lambda(X_{t-1} - \mu) + \epsilon_t \\ \end{aligned} $$
If we set \(Y_t\) to be the distance from the mean \(X_t - \mu\) then: $$ \begin{align} Y_t = \lambda Y_{t-1} + \epsilon_t \label{2} \end{align} $$
Half-life
The half-life is defined as the time \(h\) it takes for \(X_t\) to decay half way to the mean. In other words, the time \(h\) it takes for \(Y_t\) to decay halfway to \(0\). This is written as: $$ E[Y_{t+h}] = \frac{1}{2}Y_t $$ Equation \((\ref{2})\) gives us: $$ E[Y_{t+h}] = \lambda^h Y_t $$ Which means that: $$ \lambda^h Y_t = \frac{1}{2} Y_t $$
Solving for the half-life \(h\) results in: $$ h = -\frac{\log(2)}{\log(\lambda)} $$