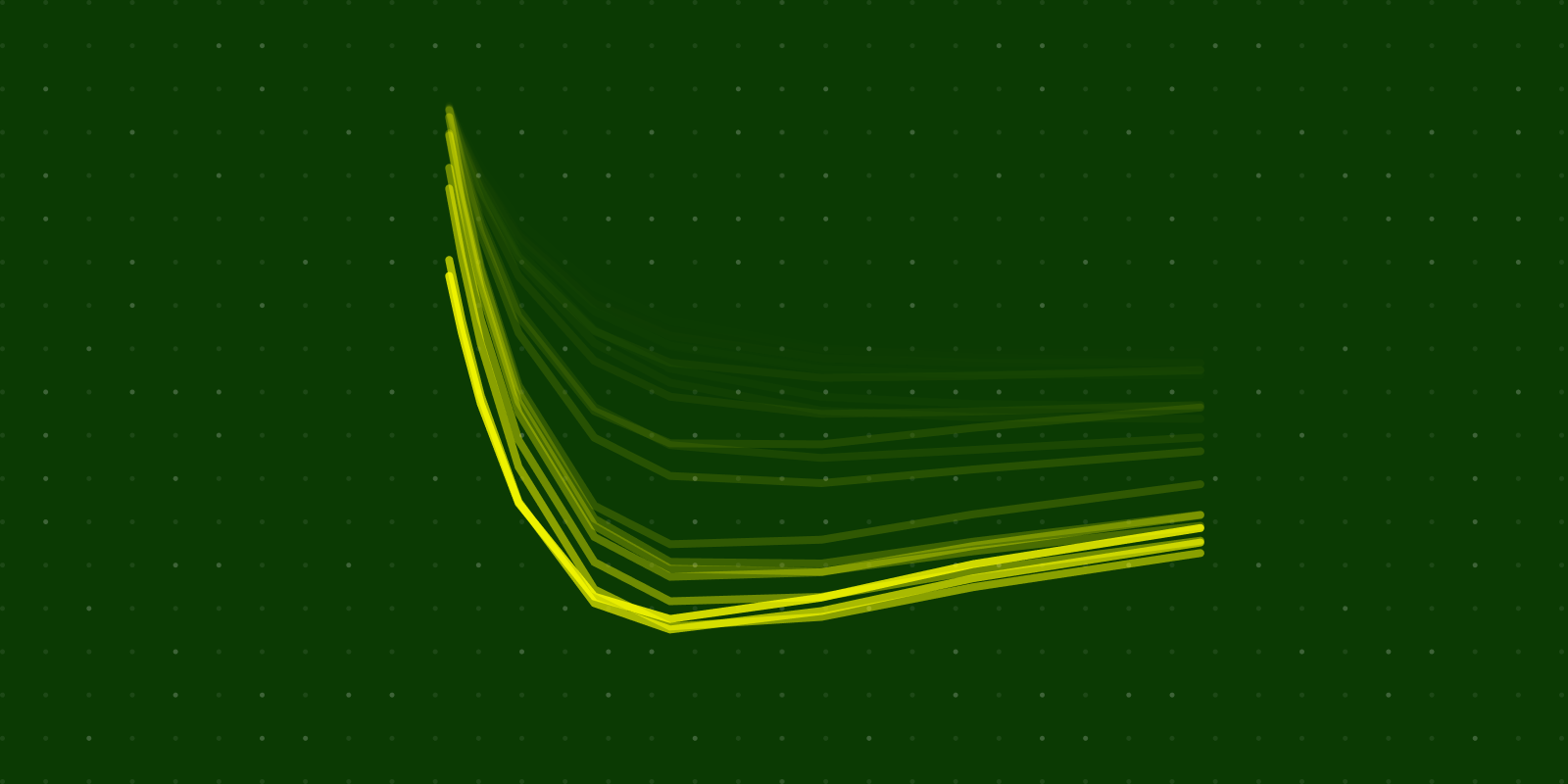
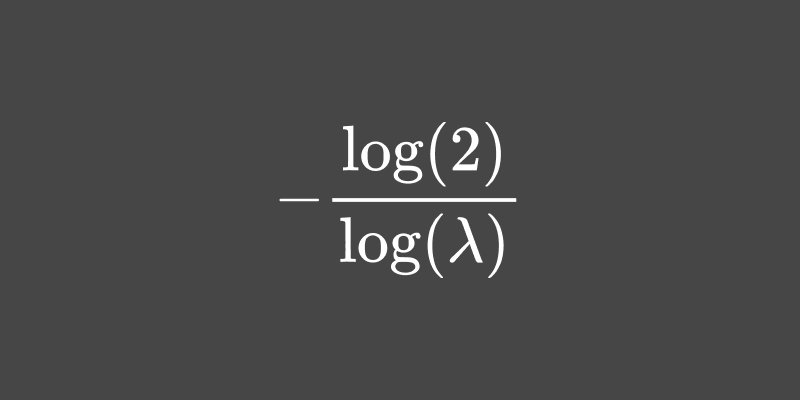Modelling the yield curve of US government treasuries
I show you how to build a factor model of US treasury yields. The factor model captures fundamental features of the whole yield curve.
Replicating Pandas exponentially weighted variance
Learn why calculating an exponentially weighted variance doesn’t yield a correct estimation of variance.
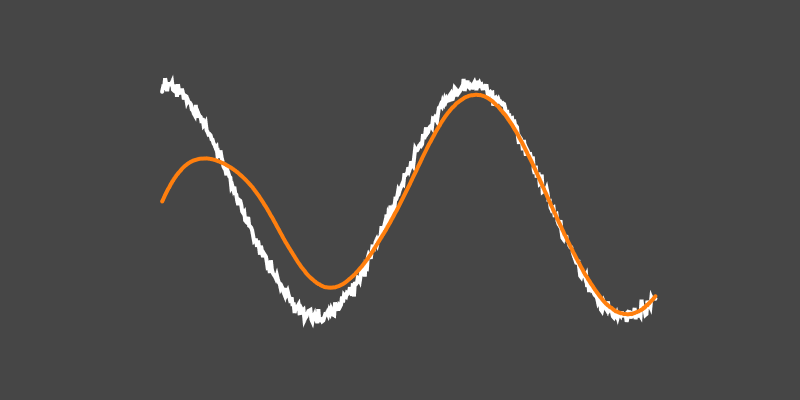
Wiener-Khinchin theorem and Gaussian processes
There’s a magical little theorem that links a power spectral density to the autocovariance function. You can use this to quickly estimate a Gaussian process of a periodic time series.
Intro to Black-Scholes, implied volatility and hedging
A break down of how the Black-Scholes option pricing model works, what implied volatility is and how you can use the model to hedge risks.
Forecasting currency rates with fractional brownian motion
Fractional Brownian motion is a stochastic process that can model mean reversion. Predicting future values turns out to be a simple linear model. This model has significant predictive power when applied to currencies.
Square root of a portfolio covariance matrix
The square root of your portfolio’s covariance matrix gives you a powerful way of understanding where your portfolio variance is coming from. Here I show how to calculate the square root and provide an interactive example to explore how it works.
Recursive least-squares linear regression
Rather than recalculating a least–squares model on each new data point, you can simply update the fitted coefficients. This saves you computational time and allows you to place greater emphasis on recent data.
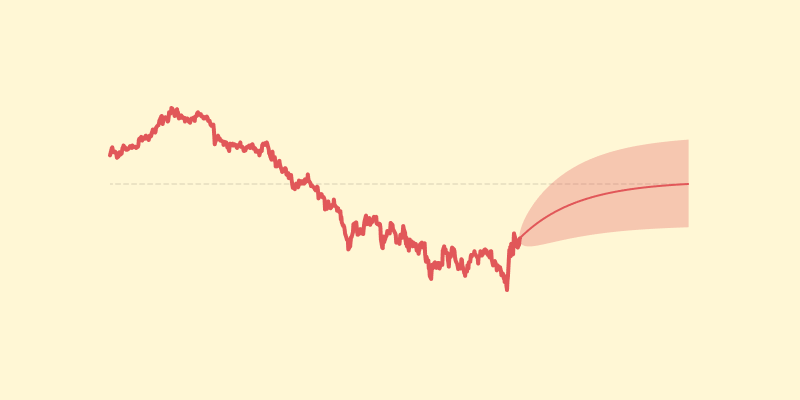
Mean reversion in government bonds
Using the Ornstein–Uhlenbeck process, you can calculate the expected spread between bond yields of different maturities. These expected values can then be used to estimated the expected value of treasury ETF spreads.
Calculating the mean and variance of bond returns
Bond returns are a function of yields. Calculating the expected value of this function is quite difficult. You can take a Taylor expansion to make calculating the mean and variance of returns much easier.
Moments of the Gaussian distribution
A reference page listing the moments of a Guassian distribution and shows how to derive co-moments.
Estimating the half-life of a time series
The half-life of a stationary series can be estimated with a linear regression. These notes show the derivation of the half-life from the regression coefficients.
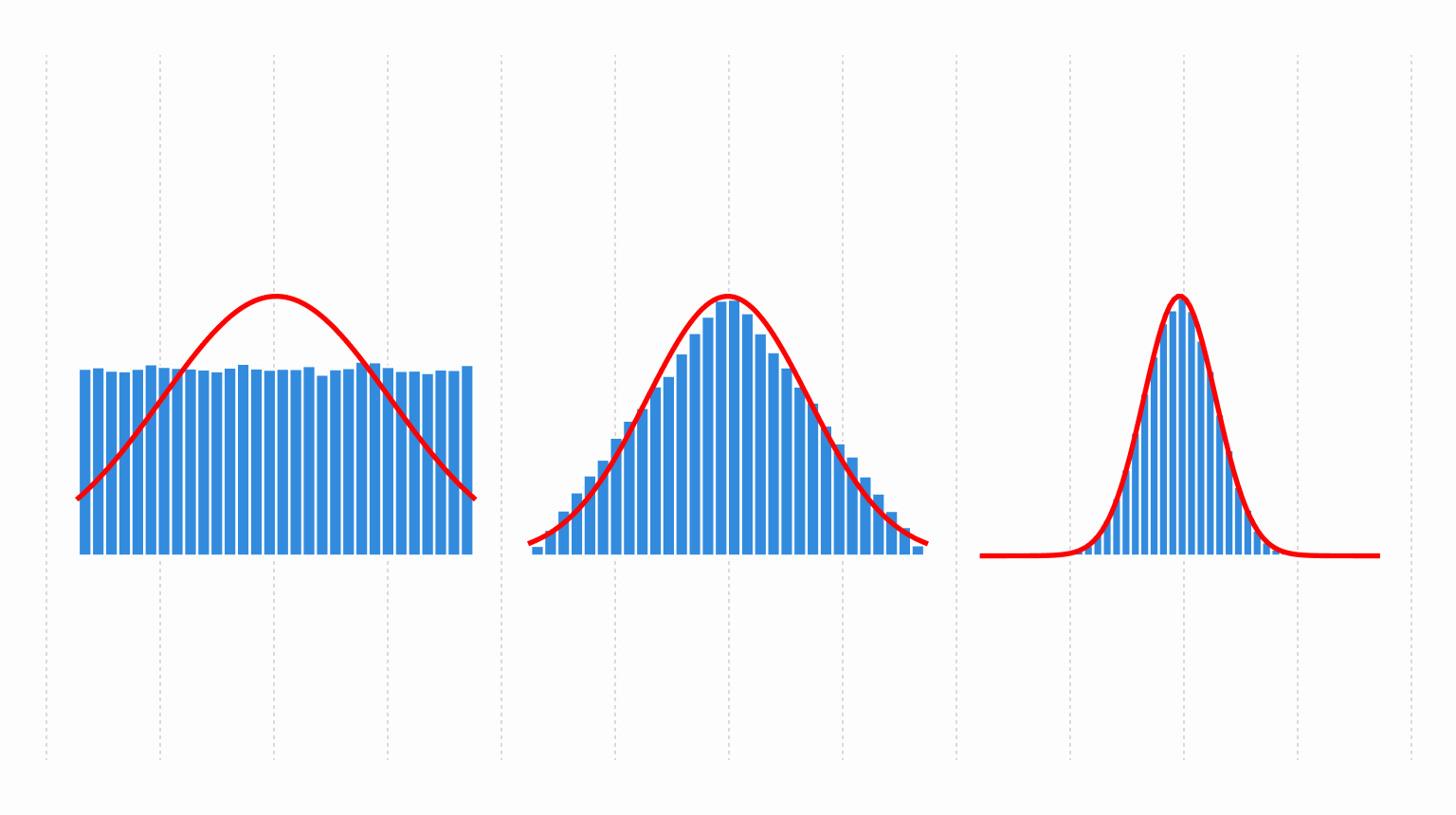
Why Returns Are Not Gaussian
Using the method of moments and building a compound distribution you can demonstrate some of the stylized facts of returns.
Understanding bond ETF returns
The return of a bond ETF can be estimated from bond yields. The distribution of a bond ETF’s returns turns out to be a function of the interest rate, expected change and variance of the interest rate. Bond returns are skewed depending on the interest rate’s level.
Fast Gaussian Kernel fit for Support Vector Regression
Support vector regression models transform input vectors into a high number of dimensions where the regression problem becomes linear. This new space is defined by a kernel function. A major drawback of these models is that they are slow to fit the kernel parameters. Here I develop an algorithm to quickly fit the Gaussian kernel’s bandwidth parameter. This algorithm is fast, robust on some datasets, and has a similar fit to slower and more exhaustive methods.
Choosing the Gaussian Kernel's Bandwidth
I created two algorithms that quickly optimise the bandwidth parameter for a Gaussian kernel. These algorithms only operate on the independent variables of a modelling task. This means they can be used regardless of the chosen kernel machine model and modelling task.